Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы. Она является важным этапом в определении механических характеристик материалов, преимущественно металлов.

Диаграмму получают экспериментально, испытывая образцы на растяжение. Для этого образцы стандартных размеров закрепляют в испытательных машинах, таких как УММ-20 или МИ-40КУ, и растягивают до разрушения. Специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой нагрузки, а самописец вычерчивает характерную для материала кривую.

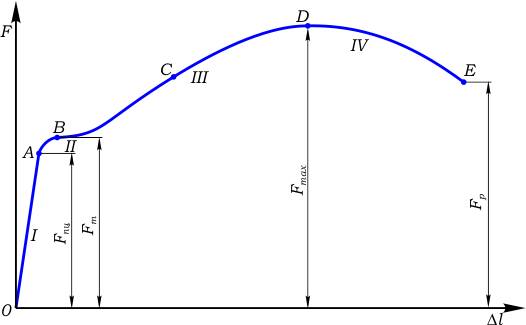
На рис. 1 представлена диаграмма для малоуглеродистой стали, построенная в системе координат F-Δl, где:

• F — продольная растягивающая сила, [Н];
• Δl — абсолютное удлинение рабочей части образца, [мм].

Как видно из рисунка, диаграмма состоит из четырех участков:

I — участок пропорциональности;
II — участок текучести;
III — участок самоупрочнения;
IV — участок разрушения.

Построение диаграммы

Рассмотрим процесс построения диаграммы более подробно.

В начале испытания на растяжение растягивающая сила F и деформация Δl стержня равны нулю, поэтому диаграмма начинается в точке пересечения осей (точка О).

На участке I до точки A диаграмма представлена прямой линией. Это означает, что деформация стержня Δl пропорциональна увеличивающейся нагрузке F.

После точки A диаграмма резко меняет направление. На участке II, начиная с точки B, линия идет почти параллельно оси Δl, что указывает на то, что деформация стержня увеличивается при почти постоянной нагрузке.

В этот момент в металле образца происходят необратимые изменения. Кристаллическая решетка металла перестраивается, и наблюдается эффект самоупрочнения.

После повышения прочности материала диаграмма снова поднимается (участок III), и в точке D растягивающее усилие достигает максимума. В рабочей части образца появляется локальное утончение, так называемая «шейка», вызванная нарушениями структуры материала (образованием пустот, микротрещин и т.д.).

Вследствие утончения и уменьшения площади поперечного сечения образца растягивающее усилие, необходимое для его растяжения, уменьшается, и кривая диаграммы опускается.

В точке E происходит разрыв образца, который происходит в сечении, где образовалась «шейка».

Работа, затраченная на разрыв образца W, равна площади фигуры, образованной диаграммой. Ее можно приблизительно вычислить по формуле:

W = 0,8Fmax∙Δlmax

По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент испытания.

Для получения механических характеристик металла диаграмму растяжения необходимо преобразовать в диаграмму напряжений.

Упругие и прочностные характеристики материалов

Диаграммы напряжений

На сегодняшний день существует несколько методик испытания материалов. Одной из самых простых и информативных является испытание на растяжение (разрыв), которое позволяет определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики. Поскольку деформация является ключевой характеристикой напряженного состояния материала, ее значение можно установить, зная размеры образца и действующие на него нагрузки.

Возникает вопрос: почему нельзя просто определить сопротивление материала? Дело в том, что абсолютно упругие материалы, разрушающиеся только после преодоления предела сопротивления, существуют лишь в теории. В реальности большинство материалов обладают как упругими, так и пластическими свойствами. Рассмотрим эти свойства на примере металлов.

Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84 с использованием стандартных образцов. Методика испытаний выглядит следующим образом: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на шаговое значение, и снова измеряется удлинение. На основании полученных данных строится график зависимости удлинений от нагрузки, называемый диаграммой напряжений.

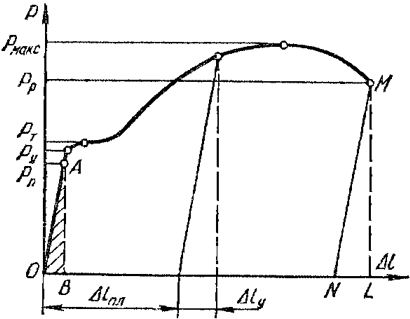
На диаграмме напряжений для стального образца выделяются пять характерных точек:

Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности равны:

σп = Рп/Fo (318.2.1)

Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:

Рп = kΔl (318.2.2)

где k — коэффициент жесткости:

k = EF/l (318.2.3)

где l — длина образца, F — площадь сечения, Е — модуль Юнга.

Модули упругости

Главные характеристики упругих свойств материалов — это модуль Юнга (E) (модуль упругости при растяжении), модуль упругости второго рода (G) (модуль упругости при сдвиге) и коэффициент Пуассона (mu) (коэффициент поперечной деформации).

Модуль Юнга Е показывает отношение нормальных напряжений к относительным деформациям в пределах пропорциональности

Модуль Юнга определяется опытным путем при испытании стандартных образцов на растяжение. Нормальные напряжения в материале рассчитываются как сила, деленная на начальную площадь сечения:

σ = Р/Fо (318.3.1), (317.2)

Относительное удлинение ε — это отношение абсолютной деформации к начальной длине:

εпр = Δl/lo (318.3.2)

Таким образом, модуль Юнга согласно закону Гука можно выразить следующим образом:

Е = σ/εпр = Plo/FoΔl = tgα (318.3.3)

Рисунок 318.2. Диаграммы напряжений некоторых сплавов металлов.

Коэффициент Пуассона μ показывает отношение поперечных деформаций к продольным

Под нагрузкой не только увеличивается длина образца, но и уменьшается площадь поперечного сечения. Если предположить, что объем материала в области упругих деформаций остается постоянным, то увеличение длины образца приводит к уменьшению площади сечения. Для образца с круглым сечением изменение площади можно выразить следующим образом:

εпоп = Δd/do (318.3.4)

Коэффициент Пуассона можно записать в виде:

μ = εпоп/εпр (318.3.5)

Модуль сдвига G показывает отношение касательных напряжений т к углу сдвига

Модуль сдвига G можно определить экспериментально, проводя испытания образцов на кручение.

При угловых деформациях сечение перемещается под углом сдвига γ к начальному сечению. Касательные напряжения вычисляются по формуле:

т = Р/F (318.3.6)

Тангенс угла наклона выражается через абсолютную деформацию Δl и расстояние h от места фиксации до точки поворота:

tgγ = Δl/h (318.3.7)

При малых значениях угла сдвига модуль сдвига можно выразить следующим образом:

G = т/γ = Ph/FΔl (318.3.8)

Модуль Юнга, модуль сдвига и коэффициент Пуассона связаны следующим соотношением:

Е = 2(1 + μ)G (318.3.9)

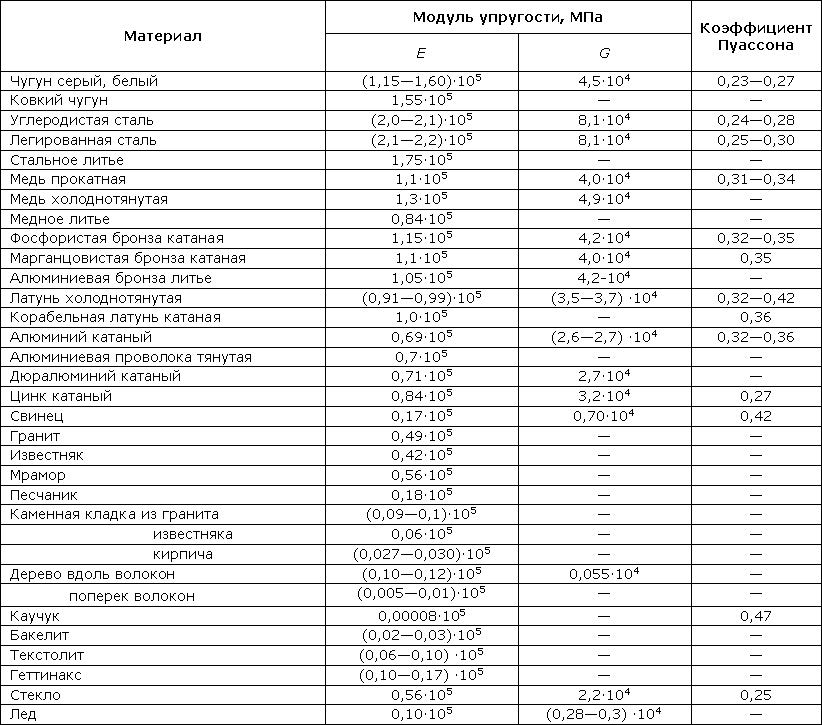
Значения постоянных Е, G и μ приведены в таблице 318.1.

Таблица 318.1. Ориентировочные значения упругих характеристик некоторых материалов

Примечание: Модули упругости являются постоянными величинами, однако технологии изготовления строительных материалов меняются. Более точные значения следует уточнять по актуальным нормативным документам. Модули упругости бетона зависят от его класса и не приводятся здесь.

Упругие характеристики определяются для различных материалов в пределах упругих деформаций, ограниченных на диаграмме напряжений точкой А. На диаграмме можно выделить несколько других точек:

2. Предел упругости Ру

Нормальные напряжения в поперечном сечении образца при достижении предела упругости равны:

σу = Ру/Fo (318.2.4)

Предел упругости определяет область, в которой пластические деформации остаются в пределах небольшой величины, установленной техническими условиями (например, 0,001%; 0,01% и т. д.). Иногда предел упругости обозначается как допуск σ0.001, σ0.01 и т. д.

3. Предел текучести Рт

σт = Рт/Fo (318.2.5)

Эта формула ограничивает участок диаграммы, где деформация увеличивается без значительного роста нагрузки (состояние текучести). В этом состоянии в объеме образца происходит частичный разрыв внутренних связей, что приводит к значительным пластическим деформациям. Материал не разрушается полностью, но его начальные геометрические размеры изменяются необратимо. На отшлифованных поверхностях образцов видны фигуры текучести — линии сдвигов, открытые профессором В. Д. Черновым. Углы наклона этих линий различаются для разных металлов и находятся в пределах 40-50°. При этом часть накопленной потенциальной энергии расходуется на частичный разрыв внутренних связей. При испытаниях на растяжение различают верхний и нижний пределы текучести — наибольшее и наименьшее напряжения, при которых возникает пластическая (остаточная) деформация при почти постоянной нагрузке.

На диаграммах напряжений отмечен нижний предел текучести. Именно этот предел для большинства материалов принимается за нормативное сопротивление материала.

Некоторые материалы не имеют четко выраженной площадки текучести. Для таких материалов условным пределом текучести σ0.2 считается напряжение, при котором остаточное удлинение образца достигает примерно 0,2%.

4. Предел прочности Рмакс (временное сопротивление)

Нормальные напряжения в поперечном сечении образца при достижении предела прочности определяются по формуле:

σв = Рмакс/Fo (318.2.6)

После превышения верхнего предела текучести (который не отображен на диаграммах напряжения) материал вновь начинает сопротивляться нагрузкам. При максимальном усилии Рмакс происходит полное разрушение внутренних связей материала. В результате пластические деформации сосредотачиваются в одном месте, образуя так называемую шейку в образце.

Напряжение при максимальной нагрузке называется пределом прочности или временным сопротивлением материала.

В таблицах 318.2 — 318.5 приведены ориентировочные пределы прочности для различных материалов:

Таблица 318.2. Ориентировочные пределы прочности на сжатие (временные сопротивления) строительных материалов.

Примечание: Для металлов и сплавов пределы прочности определяются согласно нормативным документам. Временные сопротивления для некоторых марок стали можно найти здесь.

Таблица 318.3. Ориентировочные пределы прочности (временные сопротивления) для пластмасс.

Таблица 318.4. Ориентировочные пределы прочности для волокон.

Таблица 318.5. Ориентировочные пределы прочности для древесных пород.

5. Разрушение материала Рр

Если взглянуть на диаграмму напряжений, создается впечатление, что разрушение материала происходит при уменьшении нагрузки. Это связано с тем, что при образовании «шейки» значительно меняется площадь сечения образца в этой области. Если построить диаграмму напряжений для образца из малоуглеродистой стали в зависимости от изменяющейся площади сечения, станет видно, что напряжения в рассматриваемом сечении увеличиваются до определенного предела:

Рисунок 318.3. Диаграмма напряжений: 2 — по отношению к начальной площади поперечного сечения, 1 — по отношению к изменяющейся площади сечения в районе шейки.

Однако более корректно рассматривать прочностные характеристики материала относительно площади первоначального сечения, так как в расчетах на прочность изменение геометрической формы обычно не учитывается.

Одной из механических характеристик металлов является относительное изменение ψ площади поперечного сечения в районе шейки, выражаемое в процентах:

ψ = 100(Fo — F)/Fo (318.2.7)

где Fo — начальная площадь поперечного сечения образца (до деформации), F — площадь поперечного сечения в районе «шейки». Чем больше значение ψ, тем ярче выражены пластические свойства материала. Чем меньше значение ψ, тем выше хрупкость материала.

Если сложить разорванные части образца и измерить его удлинение, то оно окажется меньше удлинения на диаграмме (длина отрезка NL), так как после разрыва исчезают упругие деформации, остаются только пластические. Величина пластической деформации (удлинения) также является важной характеристикой механических свойств материала.

За пределами упругости, вплоть до разрушения, полная деформация состоит из упругой и пластической составляющих. Если довести материал до напряжений, превышающих предел текучести (на рис. 318.1 это точка между пределом текучести и пределом прочности), а затем разгрузить его, в образце останутся пластические деформации. При повторном загружении предел упругости повысится, так как изменение геометрической формы образца в результате пластических деформаций становится результатом действия внутренних связей, а новая геометрическая форма становится начальной. Этот процесс загрузки и разгрузки можно повторять несколько раз, при этом прочностные свойства материала будут увеличиваться:

Рисунок 318.4. Диаграмма напряжений при наклепе (наклонные прямые соответствуют разгрузкам и повторным загружениям).

Такое изменение прочностных свойств материала, получаемое путем повторяющихся статических загружений, называется наклепом. Однако при повышении прочности металла за счет наклепа уменьшаются его пластические свойства, а хрупкость увеличивается, поэтому обычно считается полезным относительно небольшой наклеп.

Работа деформации

Прочность материала зависит от силы взаимодействия его частиц. Поэтому сопротивление удлинению на единицу объема можно использовать как характеристику прочности. Однако предел прочности не отражает всех прочностных свойств материала, так как он касается только поперечных сечений. При разрыве разрушаются связи по всей площади сечения, тогда как при сдвигах, возникающих при пластической деформации, разрушаются только местные связи. На разрушение этих связей затрачивается работа внутренних сил, равная работе внешних сил, необходимых для перемещения:

А = РΔl/2 (318.4.1)

где 1/2 — это среднее значение нагрузки, увеличивающейся от 0 до Р в момент приложения.

При упругой деформации работа сил определяется площадью треугольника ОАВ (см. рис. 318.1). Полная работа, затраченная на деформацию образца и его разрушение, выражается формулой:

А = ηРмаксΔlмакс (318.4.2)

где η — коэффициент полноты диаграммы, равный отношению площади всей диаграммы, ограниченной кривой АМ и прямыми ОА, MN и ON, к площади прямоугольника со сторонами 0Рмакс (по оси Р) и Δlмакс (пунктир на рис. 318.1). При этом необходимо вычесть работу, определяемую площадью треугольника MNL, относящуюся к упругим деформациям.

Работа, затрачиваемая на пластические деформации и разрушение образца, является важной характеристикой материала, определяющей его хрупкость.

Деформация сжатия

Деформации сжатия аналогичны деформациям растяжения: сначала возникают упругие деформации, затем, при превышении предела упругости, добавляются пластические. Характер деформации и разрушения при сжатии показан на рис. 318.5:

Рисунок 318.5

а — для пластических материалов; б — для хрупких материалов; в — для дерева вдоль волокон; г — для дерева поперек волокон.

Испытания на сжатие менее удобны для определения механических свойств пластических материалов из-за сложности фиксации момента разрушения. Методы механических испытаний металлов регламентируются ГОСТ 25.503-97. При испытании на сжатие форма и размеры образца могут варьироваться. Ориентировочные значения пределов прочности для различных материалов приведены в таблицах 318.2 — 318.5.

Если материал находится под постоянной нагрузкой, к мгновенной упругой деформации постепенно добавляется добавочная упругая деформация. При полном снятии нагрузки упругая деформация уменьшается пропорционально напряжениям, а добавочная упругая деформация исчезает медленнее.

Добавочная упругая деформация, возникающая при постоянном напряжении и исчезающая не сразу после разгрузки, называется упругим последействием.

Влияние температуры на изменение механических свойств материалов

Твердое состояние — не единственное агрегатное состояние вещества. Твердые тела существуют в определенном диапазоне температур и давлений. Повышение температуры вызывает фазовый переход из твердого состояния в жидкое, называемый плавлением. Температуры плавления, как и другие физические характеристики материалов, зависят от множества факторов и определяются экспериментально.

Таблица 318.6. Температуры плавления некоторых веществ

Примечание: В таблице указаны температуры плавления при атмосферном давлении (кроме гелия).

Упругие и прочностные характеристики материалов, представленные в таблицах 318.1-318.5, обычно определяются при температуре +20 °C. Согласно ГОСТ 25.503-97, испытания металлических образцов допускается проводить в диапазоне температур от +10 до +35 °C.

Изменение температуры влияет на потенциальную энергию тела и, соответственно, на внутренние силы взаимодействия. Механические свойства материалов зависят не только от абсолютной температуры, но и от времени ее воздействия. Для большинства материалов при нагреве прочностные характеристики (σп, σт и σв) уменьшаются, в то время как пластичность увеличивается. При снижении температуры прочностные характеристики возрастают, но повышается хрупкость. При нагреве модуль Юнга (Е) уменьшается, а коэффициент Пуассона увеличивается; при снижении температуры наблюдается обратный процесс.

Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.

При нагревании цветных металлов и их сплавов прочность сразу падает, и при температуре около 600 °C практически теряется. Исключение составляет алюмотермический хром, чья прочность увеличивается с повышением температуры и достигает максимума (σв1100 = 2σв20) при 1100 °C.

Характеристики пластичности меди, медных сплавов и магния уменьшаются с ростом температуры, тогда как у алюминия — увеличиваются. При нагреве пластмасс и резины предел прочности резко снижается, а при охлаждении эти материалы становятся очень хрупкими.

Влияние радиоактивного облучения на изменение механических свойств

Радиоактивное облучение по-разному влияет на материалы. Для неорганических веществ воздействие облучения на механические характеристики и пластичность схоже с понижением температуры: с увеличением дозы облучения растет предел прочности и особенно предел текучести, в то время как пластичность снижается.

Облучение пластмасс также увеличивает хрупкость. Влияние на предел прочности варьируется: у некоторых материалов, таких как полиэтилен, облучение почти не сказывается, у других, например катамена, приводит к значительному снижению прочности, а у селектрона — к ее повышению.