Содержание:

Потенциальная энергия растяжении

• Потенциальная энергия напряжения. Упругое тело, будучи деформированным, аккумулирует энергию, которая расходуется на деформацию. При снятии нагрузки эта энергия возвращается упругим телом.

Упругие аккумуляторы энергии широко используются в часовых механизмах и некоторых записывающих устройствах. Внешние силы действуют на упругое тело, создавая скорость частиц, что приводит к кинетической энергии, а также потенциальной энергии деформации.

Уравнение энергетического баланса: A = T — U. Величина U представляет собой часть работы, затраченной на деформацию тела. Если тело упругое, эта энергия сохраняется до изменения нагрузки. Для вычисления U предполагается, что внешняя сила приложена так, что кинетическая энергия T равна нулю.

В процессе деформации происходит последовательность бесконечно малых приращений удлинения d(l), вызванных увеличением силы P, что связано с законом Гука. Приращение D(A) удлинения соответствует основной работе: dA = P d(l). При консолидации от D = 0 до конечного значения D: A = ∫ P d(l).

Приведем две эквивалентные формы для выражения потенциальной энергии растяжения:
1. E = (1/2) P D
2. E = (1/2) k D²

При этом P — внешняя сила, действующая на неподвижный стержень. В динамике сила, растягивающая стержень, является суммой внешних сил и силы инерции.

Энергию упругой деформации удобно выражать на единицу объема стержня: E = (1/2) k D².

В стержне, находящемся в пластическом состоянии, работа внешних сил также расходуется на пластическую деформацию. Уравнение энергетического баланса в этом случае: A = T — U — W, где W — работа пластической деформации. Если повторить предыдущие рассуждения, U — W = ∫ P d(l).

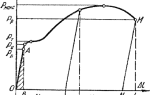
Согласно диаграмме растяжения, площадь под графиком соответствует упругой энергии, которая представлена площадью треугольника.

1. Энергию вы изучали в курсе физики 7 класса. Например, тележка, съезжающая с наклонной плоскости, передвигает брусок, совершая работу. Водитель автомобиля, нажимая на тормоза, также совершает работу против силы трения. Если тело может совершить работу, оно обладает энергией, обозначаемой буквой E. Единица энергии в СИ — джоуль (1 Дж).

2. Различают два вида механической энергии: потенциальную и кинетическую. Потенциальная энергия — это энергия взаимодействия тел, зависящая от их взаимного положения. Все взаимодействующие тела обладают потенциальной энергией, включая частицы, из которых они состоят.

3. Потенциальная энергия тела, поднятого над Землей, определяется работой силы тяжести. Если тело массой m падает с высоты h1 до h2, работа силы тяжести равна A = mgh = mg(h1 — h2). Изменение потенциальной энергии тела равно работе силы тяжести с противоположным знаком.

4. При определении потенциальной энергии необходимо указывать уровень, относительно которого она отсчитывается, называемый нулевым уровнем. Например, потенциальная энергия мяча над волейбольной сеткой отличается от его потенциальной энергии над полом спортзала, но разность не зависит от выбранного нулевого уровня.

5. Потенциальная энергия деформированного тела возникает при его сжатии или растяжении, когда изменяются силы взаимодействия между частицами. Работа силы упругости равна изменению потенциальной энергии пружины с противоположным знаком.

Вопросы для самопроверки:

1. Когда тело обладает энергией и какова единица измерения?
2. Что такое потенциальная энергия?
3. Как вычислить потенциальную энергию тела, поднятого над Землей?
4. Зависит ли потенциальная энергия от нулевого уровня?
5. Как вычислить потенциальную энергию упруго деформированного тела?

Задание 19:

1. Какую работу нужно совершить, чтобы переложить пакет с мукой массой 2 кг с высоты 0,5 м на стол на высоте 0,75 м? Каковы потенциальные энергии пакета на полке и на столе?
2. Какую работу нужно совершить, чтобы растянуть пружину жесткостью 4 кН/м на 2 см? Какова дополнительная работа для растяжения на 1 см? Каково изменение потенциальной энергии пружины в этих состояниях?
3. На графике зависимости силы тяжести от высоты мяча вычислите потенциальную энергию на высоте 1,5 м.
4. На графике зависимости удлинения пружины от силы определите потенциальную энергию при удлинении 4 см.

Энциклопедия по машиностроению XXL

Таким образом, для стержня постоянного сечения при равномерной продольной силе потенциальная энергия при растяжении (или сжатии) определяется по формуле [c.65].

Закрепим концы резинового жгута, растянем его и зафиксируем в этом состоянии. В нем останется потенциальная энергия деформации. Если отпустить один конец жгута, он вернется в исходное состояние, и потенциальная энергия деформации перейдет в кинетическую энергию. Если подставить руку под сокращающийся жгут, можно наглядно убедиться в этом переходе [c.104].

Чтобы выразить потенциальную энергию при растяжении через внутренние силы или напряжения, заметим, что ( EM D / = EI EA — N1 / (EA) N = aL U = G ). Подставляя ( Ep A_1 ) в (7.2), найдем [c.180].

Пружины винтовые — параметры и геометрия 923 — кручение 922 — жесткость 925 — конструктивные особенности и расчет 931 — крепление 933 — характеристики и потенциальная энергия 932 — растяжение 922 — конструктивные особенности и характеристики 928 [c.994].

Жесткость 925 — допускаемые напряжения 926, 927 — силы и моменты в поперечных сечениях витков 923 — потенциальная энергия 925 — растяжение-сжатие с витками круглого сечения — расчет 926, 927 [c.994].

Ранее были даны формулы для вычисления потенциальной энергии при растяжении и сжатии (10), при сдвиге (36), при кручении (52) и при чистом изгибе (63, п. г.) [c.313].

Полная потенциальная энергия температурного растяжения пластины имеет вид [c.237].

Растяжение (или сжатие) 199 — допускаемые напряжения — выбор 173, 174, 642 — нормальные напряжения 199, 258, 534, 645 — потенциальная энергия деформаций упругих 179 [c.790].

Потенциальная энергия, соответствующая растяжению поверхности раздела, будет равна [c.570].

Работа внешних сил и потенциальная энергия при растяжении [c.39].

Как вычисляется работа внешних сил и потенциальная энергия при растяжении [c.54].

Потенциальная энергия деформации складывается из энергии деформации изгиба и кручения, а также энергии деформации растяжения и сдвига срединной поверхности [c.109].

Колебания растяжения-сжатия. Простейшая форма колебаний типа растяжения-сжатия — это форма, при которой центральная линия кольца образует кольцо с периодически изменяющимся радиусом, а все поперечные сечения перемещаются в радиальном направлении без поворотов (рис. 5.33, б). Обозначим перемещение в радиальном направлении произвольной точки кольца как ( delta ). Тогда относительное удлинение кольца в окружном направлении (деформация растяжения) равно ( delta / R ). Потенциальная энергия деформации, представляющая в данном случае энергию простого растяжения, будет выражаться следующим образом [c.431].

Вследствие упругой деформации в теле накапливается потенциальная энергия. Удельная потенциальная энергия при осевом растяжении или сжатии определяется по формуле (9.6). Для объемного напряженного состояния эта энергия [c.152].

Энергетическая теория формоизменения (четвертая теория прочности) принимает в качестве критерия прочности количество удельной потенциальной энергии формоизменения, накопленной деформированным элементом. Переход материала в предельное состояние происходит, когда величина удельной потенциальной энергии формоизменения достигает значения, соответствующего предельному состоянию материала при растяжении [c.198].

Груз ( Q ) уравновешивается начальной растягивающей силой, возникающей при статических растяжениях бетона. Поэтому окончательное выражение (20.137) для потенциальной энергии системы будет таким же, как и в случае, когда ( Q = 0 ) и удлинение пружины равно ( x ) [c.576].

Определение напряжений и деформаций стержней, находящихся под действием скручивающих ударных нагрузок, целесообразно проводить через потенциальную энергию деформации скручиваемого стержня [c.640].

Работа внутренних сил, отрицательная по знаку и численно равная ей потенциальная энергия при кручении, вычисляется аналогично тому, как это делалось при растяжении (сжатии) [c.120].

При чистом сдвиге, как и при растяжении, в деформируемом теле накапливается упругая потенциальная энергия. Эту энергию можно подсчитать, рассматривая изменение формы прямоугольного элемента с размерами ( lx ), ( ly ) и толщиной ( t ) (рис. 75) [c.79].

Как вычисляется потенциальная энергия упругой деформации при растяжении (сжатии) [c.41].

Кинетическая энергия точки (изгиба, кручения, сжатия, сдвига, растяжения, пластической деформации, относительного движения, твердого тела и т. д.). Кинетическая энергия в нормальных координатах (в обобщенных координатах). Энергия в конце удара. Потенциальная энергия поля силы тяжести (поля центральных сил, пружины и т. д.) [c.29].

Для конструкционных материалов диссипация подводимой энергии позволяет противостоять разрушению, аналогичному смерти для биологических систем. Подвод энергии к конструкционным материалам осуществляется в процессе эксплуатации в виде различных нагрузок: сжатия, растяжения, изгиба, кручения и циклических нагрузок. Эта энергия называется энергией деформации, она потенциальна и приводит к деформации — изменению первоначальной формы и размеров образца материала, а также изменению его прочностных свойств [c.104].

Условие минимальности энергии гласит ( 6F + bU = 0 ), где ( U ) — потенциальная энергия в поле внешних сил. Предположим, что внешние растягивающие силы можно пренебречь по сравнению с изгибающими. Тогда для ( Delta U ) имеем то же выражение, что и в [c.77].

При обсуждении диаграммы растяжения (см. рис. 4.9) отмечалось, что при приложении нагрузки к кристаллу сначала наблюдается небольшая область упругих деформаций (закон Гука). Область упругих деформаций уменьшается с повышением температуры и становится ничтожно малой вблизи температуры плавления. В упругой области каждый атом кристалла лишь слегка смещается в направлении нагрузки из своего положения равновесия в решетке. Теория не позволяет предсказать значение предела упругости, но линейная зависимость между силой и упругой деформацией объясняется тем, что кривую потенциальной энергии взаимодействия атомов (рис. 4.11) при малых смещениях можно аппроксимировать параболой ( U = kx^2 ). Отсюда сила [c.128].

Далее тело начнет двигаться обратно с возрастающей скоростью. В положении ( x ) его скорость снова достигнет того же абсолютного значения. При дальнейшем движении скорость и кинетическая энергия упадут до нуля. Пусть это будет в положении ( xj ). Работа постоянной силы ( F ) и силы, действующей со стороны пружины, зависит только от начального и конечного положений тела, поэтому работа по любому пути всегда равна нулю. Таким образом, работа силы на пути от ( O ) до ( X2 ) и обратно от ( xj ) до ( x ) равна ( F cdot x ), поскольку ( Tz = 0 ). Эта работа должна быть равна потенциальной энергии пружины ( = frac{1}{2} kx^2 ). Решение ( 2F = kx ) невозможно, так как при растяжении, меньшем ( x ), везде ( 2F > kx ). Остается одно решение ( x = 0 ), то есть тело вернется в начальное положение. После этого все движения будут повторяться, и тело будет совершать колебания около положения ( X_i = frac{F}{k} ) в обе стороны на величину ( x ). При этом скорость тела будет изменяться от нуля (в крайних точках) до [c.168].

Потенциальная энергия деформации, накопленная брусом при кручении, может быть определена аналогично тому, как это было сделано при растяжении [c.237].

Процесс разрыва жидкой пленки требует определенного времени. В каждой точке диска в потенциальной зоне разрыва границе устойчивости будет соответствовать такое состояние, когда импульс кинетической энергии крупной волны компенсирует затраты энергии на растяжение пленки и предотвращает разрыв. Если время между прохождением двух волн не превышает времени разрушения пленки, то выступы, незначительно превышающие общий уровень, не приведут к разрушению пленки [c.287].

Полная энергия ( E = E0 — Ef ). 87% всей потенциальной энергии при растяжении идет на изменение формы стержня, и только 3% — на изменение объема [c.87].

Энергия потенциальная 35. Пружины цилиндрические винтовые растяжения-сжатия — напряжения остаточные 69, 70 — обжатие пластическое 71 — расчет 68-71 [c.403].

Для определения осевого перемещения и напряжений в сильфоне воспользуемся энергетическим методом. Полная потенциальная энергия определяется как сумма потенциальной энергии деформаций и потенциала внешних сил. Потенциальная энергия деформаций ( A ) является суммой энергии растяжения срединной поверхности и энергии изгиба ( A_i ) [c.20].

По данным предыдущей задачи определим, применив гипотезу удельной потенциальной энергии формоизменения, коэффициент запаса прочности винта машины при растяжении образца силой ( Q = 5-10 ) кГ. Материал винта — сталь 45 [c.261].

Критерий удельной потенциальной энергии формоизменения (четвертая теория прочности) принимает в качестве критерия прочности количество удельной потенциальной энергии формоизменения, накопленной деформированным элементом. Опасное состояние (текучесть) наступает, когда удельная потенциальная энергия формоизменения достигает предельного значения, которое можно определить при простом растяжении в момент текучести [c.186].

Потенциальная энергия деформации, накопленная брусом при кручении, определяется аналогично тому, как это делалось в случае растяжения. Рассмотрим участок закрученного бруса длиной ( l ) [c.88].

Сила, растягивающая пружину, совершает работу и увеличивает потенциальную энергию пружины. Если растягивать пружину медленно, работа внешней силы равна увеличению потенциальной энергии пружины. Для медленного растяжения достаточно приложить к пружине (с закрепленным неподвижно другим концом) постепенно увеличивающуюся силу ( F ), которая немного превышает силу, действующую со стороны пружины. Если затем пружина будет сжиматься, она совершит такую же работу, какую совершила внешняя сила при растяжении. Следовательно, при медленном растяжении работа внешней силы равна увеличению потенциальной энергии системы. При быстром растяжении это не будет иметь места, так как для значительного ускорения конца пружины внешняя сила ( F ) должна быть значительно больше силы, действующей со стороны пружины, и тогда работа внешней силы будет больше, чем увеличение потенциальной энергии пружины. Только при медленных движениях работа внешних сил равна увеличению потенциальной энергии системы [c.131].

Начнем с простейшего случая, когда на тело действуют только упругие силы. Определим, устойчиво ли состояние равновесия, в котором находится точка ( O ) на рис. 62, когда правый конец пружины закреплен так, что обе пружины несколько растянуты. Для равновесия силы, с которыми действуют пружины на точку ( O ), должны быть равны, поэтому удлинения пружин в состоянии равновесия связаны соотношением ( F = kx ). Отсчитывая смещения ( x ) точки ( O ) относительно положения равновесия, найдем выражение общей потенциальной энергии двух пружин как функцию ( X ) [c.134].

В качестве примера подсчитаем потенциальную энергию упругодеформированной пружины (рис. 38, а). По закону Гука упругая сила пропорциональна смещению и противоположна ему по направлению: ( F_{упр} = -kx ). Элементарная работа, совершаемая упругой силой при растяжении пружины на ( dx ), равна [c.53].