Внутренние усилия при растяжении-сжатии.

Осевое растяжение или сжатие прямого бруса происходит под воздействием внешних сил, вектор равнодействующей которых совпадает с осью бруса. При этом в поперечных сечениях возникают только продольные силы N. Значение продольной силы N в определённом сечении равно алгебраической сумме проекций всех внешних сил, действующих с одной стороны от этого сечения. По принятому правилу знаков, положительные продольные силы N возникают от растягивающих нагрузок, а отрицательные — от сжимающих (рис. 5).

Для определения участков стержня или его сечений с максимальным значением продольной силы строят эпюру продольных сил, используя метод сечений, подробно описанный в статье:

Анализ внутренних силовых факторов в статистически определимых системах.

Рекомендую также ознакомиться с статьёй:

Расчёт статистически определимого бруса.

Изучив теорию и задачи по приведённым ссылкам, вы сможете глубже понять тему «Растяжение-сжатие».

Напряжения при растяжении-сжатии.

Продольная сила N, определенная методом сечений, является равнодействующей внутренних усилий, распределенных по поперечному сечению стержня (рис. 2, б). Согласно определению напряжений, можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.

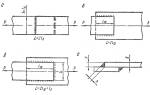
Чтобы определить нормальные напряжения в любой точке бруса, необходимо знать закон их распределения по поперечному сечению. Экспериментальные исследования показывают, что если на поверхность стержня нанести ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии остаются параллельными (рис. 6, а). Это явление описывается гипотезой плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Поскольку все продольные волокна стержня деформируются одинаково, напряжения в поперечном сечении также равны. Эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис. 6, б. Напряжения равномерно распределены по поперечному сечению, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения в поперечных сечениях растянутого или сжатого бруса равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения считаются положительными при растяжении и отрицательными при сжатии.

Деформации при растяжении-сжатии.

Рассмотрим деформации, возникающие при растяжении и сжатии стержня (рис. 6, а). Под действием силы F брус удлиняется на величину Δl, называемую абсолютным удлинением или абсолютной продольной деформацией. Она равна разности длины бруса после деформации l1 и его первоначальной длины l.

Отношение абсолютной продольной деформации Δl к первоначальной длине l называется относительным удлинением или относительной продольной деформацией. При растяжении продольная деформация положительна, а при сжатии — отрицательна. Для большинства конструкционных материалов в стадии упругой деформации выполняется закон Гука, который устанавливает линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости E, также известный как модуль упругости первого рода, является коэффициентом пропорциональности между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).

Таблица 1

Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации. Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Экспериментально установлено, что в пределах действия закона Гука поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации или коэффициентом Пуассона μ.

Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const, и для различных материалов коэффициент Пуассона варьируется от 0 до 0,5 (табл. 2).

Таблица 2

Коэффициент Пуассона

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N. Эту формулу можно использовать для вычисления абсолютного удлинения участка стержня длиной l при условии, что продольная сила в этом участке постоянна. Если продольная сила N изменяется, Δl определяют интегрированием в пределах этого участка.

Произведение (E·A) называется жесткостью сечения стержня при растяжении или сжатии.

Механические свойства материалов.

Основные механические свойства материалов при деформации включают прочность, пластичность, хрупкость, упругость и твердость.

Прочность — это способность материала сопротивляться внешним силам без разрушения и появления остаточных деформаций.

Пластичность — свойство материала выдерживать большие остаточные деформации без разрушения. Остаточные деформации, которые сохраняются после снятия нагрузки, называются пластическими.

Хрупкость — это свойство материала разрушаться при малых остаточных деформациях (например, чугун, бетон, стекло).

Идеальная упругость — способность материала полностью восстанавливать свою форму и размеры после устранения причин деформации.

Твердость — это свойство материала сопротивляться проникновению других тел.

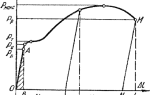
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длиной ( l0 ) и постоянным поперечным сечением площади ( A0 ) растягивается с обоих торцов силой ( F ).

Диаграмма сжатия стержня представлена на рисунке 10, а.

Здесь ( Delta l = l — l0 ) — абсолютное удлинение стержня; ( varepsilon = Delta l / l0 ) — относительное продольное удлинение; ( sigma = F / A0 ) — нормальное напряжение; ( E ) — модуль Юнга; ( sigmap ) — предел пропорциональности; ( sigma{уп} ) — предел упругости; ( sigma{т} ) — предел текучести; ( sigma{в} ) — предел прочности (временное сопротивление); ( varepsilon{ост} ) — остаточная деформация после снятия нагрузок.

Для материалов без ярко выраженной площадки текучести вводят условный предел текучести ( sigma{0,2} ) — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение диаметра («шейка»). Дальнейшее удлинение происходит в зоне шейки (зона местной текучести). При достижении напряжением предела текучести ( sigma{т} ) поверхность стержня становится матовой, на ней появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.

Опасным сечением при растяжении и сжатии называют поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σпред — предельное напряжение (σпред = σт для пластических материалов и σпред = σв для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2–2,5; для хрупких материалов [n] = [nв] = 2–5, а для древесины [n] = 8–12.

Расчеты на прочность при растяжении и сжатии.

Цель расчета конструкции — оценить ее эксплуатационную пригодность при минимальных затратах материалов. Это отражается в методах расчета прочности и жесткости.

Условие прочности стержня при растяжении (или сжатии):

При проектировании определяется площадь опасного сечения стержня.

Для расчета допускаемой нагрузки вычисляется допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.

Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно соответствовать установленному условию.

Также часто проводят расчет жесткости отдельных участков стержня.

Следующая важная тема теории — изгиб балки.

Техническая механика

Сопротивление материалов

Деформации при растяжении и сжатии

Продольные деформации при растяжении и сжатии

Характер деформаций, которым подвергается прямой брус при растяжении или сжатии, мы определили, проведя опыт с резиновым брусом, на который была нанесена сетка линий.

Рассмотрим брус постоянного сечения длиной l, один конец которого зафиксирован, а к свободному концу приложена растягивающая сила F. Под действием этой силы брус удлинится на величину Δl, которую назовем абсолютным удлинением.

Отношение абсолютного удлинения Δl к первоначальной длине бруса l называется относительным удлинением и обозначается ε:

ε = Δl / l

Относительное удлинение — безразмерная величина, иногда выражаемая в процентах.

Таким образом, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.

Закон Гука при растяжении и сжатии

Напряжения и деформации при растяжении и сжатии связаны линейной зависимостью, известной как закон Гука, названный в честь английского физика Р. Гука (1653-1703), который его установил.

Закон Гука формулируется так: нормальное напряжение пропорционально относительному удлинению или укорочению.

Математически это записывается как:

σ = E ε.

Здесь E — коэффициент пропорциональности, характеризующий жесткость материала бруса, то есть его способность сопротивляться деформации. Этот коэффициент называется модулем продольной упругости или модулем упругости первого рода.

Модуль упругости, как и напряжение, измеряется в паскалях (Па).

Значения E для различных материалов устанавливаются экспериментально и могут быть найдены в справочниках. Например, для стали E = (1,96…2,16) х 10^5 МПа, для меди E = (1,00…1,30) х 10^5 МПа и так далее.

Важно отметить, что закон Гука справедлив только в определенных пределах нагружения.

Подставив в формулу закона Гука значения относительного удлинения и напряжения: ε = Δl / l и σ = N / A, получаем следующую зависимость:

Δl = Nl / (E A).

Произведение модуля упругости на площадь сечения E×A, находящееся в знаменателе, называется жесткостью сечения при растяжении и сжатии. Оно характеризует как физико-механические свойства материала бруса, так и геометрические размеры его поперечного сечения.

Эту формулу можно интерпретировать так: абсолютное удлинение или укорочение бруса пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения.

Выражение E A / l обозначает жесткость бруса при растяжении и сжатии.

Приведенные формулы закона Гука действуют только для брусьев и их участков с постоянным поперечным сечением, изготовленных из одного материала и при постоянной силе. Для бруса с несколькими участками, отличающимися материалом, размерами сечения и продольной силой, изменение длины всего бруса определяется как алгебраическая сумма удлинений или укорочений отдельных участков:

Δl = Σ (Δli).

Поперечные деформации при растяжении и сжатии

Опыт с резиновым брусом, на котором нанесена сетка линий, показал, что при растяжении поперечные размеры бруса уменьшаются, а при сжатии — увеличиваются. Это явление наблюдается у брусьев из различных материалов.

Экспериментально установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций для данного материала остается постоянным.

Впервые на эту зависимость указал французский ученый С. Пуассон (1781-1840). Она математически записывается как:

|ε1| = ν |ε|,

где ν — коэффициент поперечной деформации, известный как коэффициент Пуассона.

Коэффициент Пуассона является безразмерной величиной и характеризует упругие свойства материала. При растяжении и сжатии его значение считается одинаковым.

Значения коэффициента Пуассона для различных материалов определены экспериментально и могут быть найдены в справочниках.

Потенциальная энергия деформации при растяжении

При статическом растяжении образца растягивающая сила F увеличивается от нуля до определенного значения, удлиняя образец на величину Δl и совершая работу W. Эта работа аккумулируется в образце в виде потенциальной энергии деформации U. Пренебрегая незначительными потерями энергии, можно считать, что W = U.

Изучение диаграмм растяжения образцов показало, что потенциальная энергия упругой деформации стержня длиной l с постоянным поперечным сечением A при равномерной продольной силе N = F равна:

U = W = F Δl / 2 = N² l / (2E A)

В сопротивлении материалов также используется понятие удельной потенциальной энергии деформации, которая рассчитывается как потенциальная энергия на единицу объема бруса.

При одновременном действии растягивающих и сжимающих нагрузок или изменении размеров поперечного сечения бруса, его разбивают на однородные участки, и для каждого подсчитывают потенциальную энергию деформации. Общая потенциальная энергия деформации бруса определяется как сумма потенциальных энергий отдельных участков.

Анализируя формулу потенциальной энергии деформации, можно заключить, что эта величина всегда положительна, так как в ее выражении присутствуют квадраты линейных и силовых величин. Поэтому при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил, поскольку квадрат суммы не равен сумме квадратов слагаемых.

Единицей измерения потенциальной энергии деформации, как и работы, является джоуль (Дж).

---

Материалы раздела «Растяжение и сжатие»:

• Основные понятия о деформации растяжения и сжатия.
• Расчеты на прочность при растяжении и сжатии. Статически неопределимые задачи.

Смятие

Правильные ответы на вопросы Теста № 5

№ вопроса	1	2	3	4	5	6	7	8	9	10
Правильный вариант ответа	3	3	1	2	1	3	2	2	1	1

Тема 2.2. Растяжение и сжатие. Продольные и поперечные деформации. Закон Гука

Иметь представление о продольных и поперечных деформациях и их взаимосвязи.

Знать закон Гука, зависимости и формулы для расчета напряжений и перемещений.

Уметь проводить расчеты на прочность и жесткость статически определимых брусьев при растяжении и сжатии.

Рассмотрим деформацию бруса под действием продольной силы F (рис. 21.1).

В сопротивлении материалов деформации рассчитываются в относительных единицах. Существует зависимость между продольными и поперечными деформациями:

где μ — коэффициент поперечной деформации (коэффициент Пуассона), характеризующий пластичность материала.

В пределах упругих деформаций деформации пропорциональны нагрузке:

где F — действующая нагрузка; к — коэффициент. В современной форме:

Получаем зависимость:

где Е — модуль упругости, характеризующий жесткость материала.

В пределах упругости нормальные напряжения пропорциональны относительному удлинению.

Значение Е для сталей составляет (2 — 2,1) • 10^5 МПа. При прочих равных условиях, чем жестче материал, тем меньше он деформируется.

Используем известные формулы.

Относительное удлинение:

Получаем зависимость между нагрузкой, размерами бруса и возникающей деформацией:

где

Δl — абсолютное удлинение, мм;

σ — нормальное напряжение, МПа;

l — начальная длина, мм;

Е — модуль упругости материала, МПа;

N — продольная сила, Н;

А — площадь поперечного сечения, мм².

Произведение АЕ называют жесткостью сечения.

1. Абсолютное удлинение бруса пропорционально величине продольной силы, длине бруса и обратно пропорционально площади поперечного сечения и модулю упругости.

2. Связь между продольной и поперечной деформациями зависит от свойств материала и определяется коэффициентом Пуассона. Для стали μ составляет от 0,25 до 0,3; для пробки μ = 0; для резины μ = 0,5.

3. Поперечные деформации меньше продольных и редко влияют на работоспособность детали; при необходимости поперечная деформация рассчитывается через продольную.

где Δа — поперечное сужение, мм;

ао — начальный поперечный размер, мм.

4. Закон Гука выполняется в зоне упругих деформаций, определяемой при испытаниях на растяжение по диаграмме растяжения (рис. 21.2). При работе пластические деформации не должны возникать, упругие деформации малы по сравнению с геометрическими размерами тела. Основные расчеты в сопротивлении материалов проводятся в зоне упругих деформаций, где действует закон Гука.

На диаграмме (рис. 21.2) закон Гука действует от точки 0 до точки 1.

5. Определение деформации бруса под нагрузкой и сравнение ее с допускаемой (не нарушающей работоспособности бруса) называется расчетом на жесткость.

Пример 1. Дана схема нагружения и размеры бруса до деформации (рис. 21.3). Брус защемлен, необходимо определить перемещение свободного конца.

Решение:

1. Брус ступенчатый, поэтому строим эпюры продольных сил и нормальных напряжений. Делим брус на участки нагружения, определяем продольные силы и строим эпюру продольных сил.

2. Определяем величины нормальных напряжений по сечениям с учетом изменений площади поперечного сечения. Строим эпюру нормальных напряжений.

3. На каждом участке определяем абсолютное удлинение. Результаты суммируем.

Примечание. Балка защемлена, в заделке возникает неизвестная реакция в опоре, поэтому расчет начинаем со свободного конца (справа).

Пример 2. Для заданного ступенчатого бруса (рис. 2.9, а) построить эпюры продольных сил и нормальных напряжений по его длине, а также определить перемещения свободного конца и сечения С, где приложена сила Р2. Модуль продольной упругости материала Е = 2,1 • 10^5 Н/мм³.

Решение:

1. Заданный брус имеет пять участков I, II, III, IV, V (рис. 2.9, а). Эпюра продольных сил показана на рис. 2.9, б.

2. Вычислим напряжения в поперечных сечениях каждого участка.

3. Перемещение свободного конца бруса определяется как алгебраическая сумма удлинений (укорочений) всех его участков.

4. Перемещение сечения С, в котором приложена сила Р2, определяется аналогично.

5. Вычисленные значения перемещений можно получить и другим способом, определяя перемещения от действия каждой из сил Р1, Р2, Р3 в отдельности и суммируя результаты.

Пример 3. Определить напряжение в стальном стержне длиной l = 200 мм, если после приложения растягивающих сил его длина стала l1 = 200,2 мм. Е = 2,1 • 10^6 Н/мм².

Решение:

1. Абсолютное удлинение стержня.
2. Продольная деформация стержня.
3. Согласно закону Гука.

Пример 4. Стенной кронштейн (рис. 2.10, а) состоит из стальной тяги АВ и деревянного подкоса ВС. Площадь поперечного сечения тяги F1 = 1 см², площадь сечения подкоса F2 = 25 см². Определить горизонтальное и вертикальное перемещения точки В, если в ней подвешен груз Q = 20 кН. Модули продольной упругости стали Eст = 2,1 • 10^5 Н/мм², дерева Ед = 1,0 • 10^4 Н/мм².

Решение:

1. Для определения продольных усилий в стержнях АВ и ВС вырезаем узел В. Предполагаем, что стержни растянуты, направляем усилия N1 и N2 от узла (рис. 2.10, б). Составляем уравнения равновесия.

2. Вычисляем удлинение стальной тяги Δl1 и укорочение подкоса Δl2.

3. Для определения перемещения точки В мысленно разъединим стержни в шарнире и отметим их новые длины. Новое положение точки В определится при сведение деформированных стержней.

4. На рис. 2.10, г диаграмма перемещений точки В изображена в более крупном масштабе.

5. Горизонтальное и вертикальное перемещения точки В определяются по соответствующим формулам.

1. Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Каково относительное удлинение? Каково относительное сужение? (μ = 0,25.)
2. Что характеризует коэффициент поперечной деформации?
3. Сформулируйте закон Гука в современной форме при растяжении и сжатии.
4. Что характеризует модуль упругости материала? Какова единица измерения модуля упругости?
5. Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?
6. Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?
7. Ответьте на вопросы тестового задания.