В производстве металлоконструкций самым надежным методом соединения деталей является сварка. Прочность соединения обеспечивается межмолекулярным взаимодействием, возникающим при высокой температуре. Для получения качественных стыков (дорожек, швов) необходимо правильно выполнить расчеты сварного шва. Точные вычисления помогают выбрать основные и расходные материалы, а также оценить надежность и монолитность конструкции.

Расчет сварного шва на срез выполняется по общепринятым стандартным формулам.

Какие параметры используются в расчете

Для расчета прочности сварных соединений необходимо учитывать ряд показателей, что позволяет минимизировать погрешности в расчетах. Основные параметры включают:

• Ry — сопротивление материала изделия с учетом предела текучести; постоянная величина для каждого металла.
• Ru — сопротивление материала по временным характеристикам; стандартный табличный показатель.
• Rwy — сопротивление с учетом предела текучести.
• N — предельно допустимая нагрузка, которую может выдержать соединение.
• t — минимальная толщина соединяемых деталей.
• lw — максимальная длина сварного стыка, которая уменьшается на 2t при вычислении.
• gс — коэффициент условий на рабочем месте; стандартизированный параметр, присутствующий в общепринятых таблицах, включая методички для сварщиков.

Процесс растяжения и сжатия металла вычисляется по формуле.

Если детали изготавливаются из разных металлов, в формулах используются значения Ry и Ru для материала с наименьшей прочностью. То же самое касается расчета шва на срез.

Кроме указанных показателей, на надежность соединения влияют:

• качество материала изделия;
• правильно подобранные расходные материалы (присадки, электроды);
• режим сварки, включая полярность и силу тока;
• тщательность обработки заготовок — на кромке стыков не должно быть деформаций и посторонних вкраплений;
• соответствие сварного аппарата требуемой технологии сварки и мощности.

Эти характеристики обязательно учитываются, так как от них зависит точность расчета качества соединения.

Коэффициент прочности шва

Это показатель φ, который представляет собой отношение прочностей сварной дорожки и основного материала. Его значение нормируется в зависимости от способа сварки и конструкции стыка. Оно определяется согласно Правилам Госгортехнадзора и отражается в приложениях ГОСТов Р52857.1-2007, 14249-89 и 34233.1-2017.

Таблица 1. Коэффициенты прочности сварочных швов

Тип сварного соединения	Значение φ
Контролируемый участок от общей протяженности шва:
100%	10-50 %
Стыковое одностороннее, выполненное ручной сваркой	0,9	0,65
Тавровое с конструктивно предусмотренным зазором между деталями	0,8	0,65
Встык одностороннее с подкладкой из флюса или керамики, выполненное автоматической или полуавтоматической сваркой	0,9	0,8
Втавр или встык со сплошным двусторонним проваром, выполненный автоматикой или полуавтоматикой	1,0	0,9
Стыковое с подвариванием корня шва или тавровый со сплошным проваром с двух сторон, выполненные ручной сваркой	1,0	0,9
Одностороннее встык с металлической подкладкой, прилегающей к основному материалу по всей длине шва	0,9	0,8

Коэффициент прочности для дорожек, паянных мягкими и твердыми припоями с использованием аппаратов из цветных металлов, составляет 0,7 для композиционной пайки и 1 для однородной.

Используемые формулы

Существует множество формул для расчета качественных сварных швов. В расчетах учитываются не только тип шва, но и вид и толщина основного материала, площадь и расположение стыкуемых деталей, предельные нагрузки, эксплуатационная температура изделия и другие параметры. Уравнения для различных типов сварных швов различаются.

Расчет прочности швов на выпуклых поверхностях

В производстве сосудов и труб различной емкости используются стыковые сварные соединения. К ним относятся швы на выпуклых днищах (меридиональные и хордовые) и на обечайках (продольные). Стандарты и методы расчета прочности таких изделий изложены в ГОСТ 34233.11-2017. Расчет сварного соединения выпуклой поверхности зависит от нескольких факторов: марки и толщины стали, внутреннего и внешнего давления на стенки, типа нагрузки и других параметров.

Уравнение для расчета допустимого напряжения (в МПа) на примере цилиндрической обечайки сосуда, работающего при однократных статических нагрузках и изготовленного из низколегированной или углеродистой стали:

Эта формула применяется только для сосудов из пластичных материалов в условиях использования металлов.

Зависимость от типа сварочного шва

Существует несколько способов соединения металлических элементов в единую конструкцию. По расположению соединяемых деталей различают следующие виды сварных швов:

1. Стыковой — наиболее рациональный, так как минимизирует концентрацию напряжений в шве. Здесь свариваются торцы деталей, и одна часть изделия продолжает другую.
2. Угловой — элементы располагаются перпендикулярно друг другу. Прочность соединения зависит от правильно рассчитанного предельного усилия.
3. Тавровый — аналогичен угловому, но детали свариваются торцами. Этот шов прочный, экономичный и простой в выполнении.
4. Нахлесточный — края соединяемых деталей накладываются друг на друга. Этот тип укрепляет соединение и используется для сварки металла толщиной до 5 мм.

Для каждого типа расчет производится по индивидуальной формуле.

Перед началом вычисления прочности соединения необходимо рассчитать площадь его поперечного сечения. Для этого длину сварного соединения умножают на его толщину.

Соединение листов внахлест

Для расчета напряжения среза используется формула:

,

где:

• P — нагрузка на шов, Н;
• [τ]’ср — допускаемое напряжение на срез, Па;
• 0,7k — толщина шва в наиболее опасном сечении, см;
• l — длина сварной дорожки, мм.

При соединении внахлест разделка кромок не требуется.

Из формулы следует, что напряжение на срез должно быть меньше максимально допустимого.

Значение нагрузки P определяется следующим образом:

.

При расчете учитывается минимальная площадь сечения сварной дорожки. Это важно, так как прочность сварочных материалов может превышать прочность основного металла.

Угловые конструкции

Соединения рассчитываются по их поперечному сечению, принимая наименьшее значение, то есть в наиболее опасном месте дорожки. Показатель устойчивости простого углового шва на изгиб, нагруженного моментом M, вычисляется по формуле:

[ Wc = frac{M}{sigma} ]

где:

• Wc — момент сопротивления опасного сечения дорожки (шва);
• M — изгибающий момент.

Напряжение простого углового соединения на срез определяется следующим образом:

[ tau = frac{M}{Fc} ]

где:

• M — нагружающий момент на срез;
• Fc = 0,7kl — площадь сечения дорожки в опасном месте, мм²;
• P — допустимая нагрузка на дорожку.

При расчете угловых сварных швов на срез используется следующее выражение:

[ N = frac{Rwf cdot kf cdot Ywf}{betaf cdot betaz} ]

где:

• N — максимальная нагрузка на линию сцепления;
• c — коэффициент условий рабочей среды, указанный в стандартизированных таблицах;
• βf, βz — постоянные величины, не зависящие от марки металла (βz = 1, βf = 0,7);
• Rwf — сопротивление срезу, табличная величина для различных материалов;
• Rwz — сопротивление на линии стыка, стандартные табличные величины;
• kf — толщина дорожки, измеряемая по линии сплавления;
• Ywf — для стыка материала с сопротивлением 4200 кгс/см² составляет 0,85;
• Ywz — 0,85 для всех марок стали;
• lw — общая длина стыка, уменьшенная на 10 мм.

При определении длины сварочного сцепления на отрыв обязательно учитывается сила, направленная к центру тяжести. Площадь сечения выбирается в самом опасном месте дорожки, то есть наименьшая.

Тавровые швы

Условие прочности сцепления в тавре, выполненном встык и работающем на растяжение Р и момент M, выглядит так:

.

Для углового шва, который не является стыковым, формула будет следующей:

.

Тавровые швы могут быть односторонними или двусторонними.

Если тавровое соединение нагружено изгибом и крутящим моментом, используется уравнение:

.

Крутящая и изгибающая силы определяются следующими формулами:

и

.

Сварка на стыке

Расчет шва встык, работающего на сжатие или растяжение, выполняется по уравнению:

[ sigma = frac{P}{l cdot s} ]

где:

• ( l ) — длина сварочной дорожки, мм;
• ( P ) — нагрузка на стык, Н;
• ( s ) — толщина соединяемых деталей, мм;
• ( [sigma]’_{р1сж1} ) — допускаемое напряжение на растяжение или сжатие, Па.

Допустимая нагрузка ( P ) составит:

[ P{доп} = [sigma]’{р1сж1} cdot l cdot s ]

Стыковое сцепление, работающее на изгиб, рассчитывается по формуле:

[ sigma{изг} = frac{M}{Wc} ]

где:

• ( M ) — изгибающий момент, Н·мм;
• ( W_c ) — момент сопротивления расчетного сечения.

Если напряжение шва возникает как от изгиба ( M ), так и от сжатия или растяжения ( P ), то оно определяется уравнением:

[ sigma{общ} = sigma{изг} + sigma_{сж} ]

Методика расчета сварных соединений

Расчет прочности швов соединений, нагружаемых осевыми силами

Условные обозначения:

• Р — нагрузка соединения;
• L — общая длина шва;
• δ — толщина соединяемых деталей;
• k — катет углового шва;
• d, i — диаметр пробок и их количество в пробочном соединении;
• а — ширина шва при роликовой сварке.

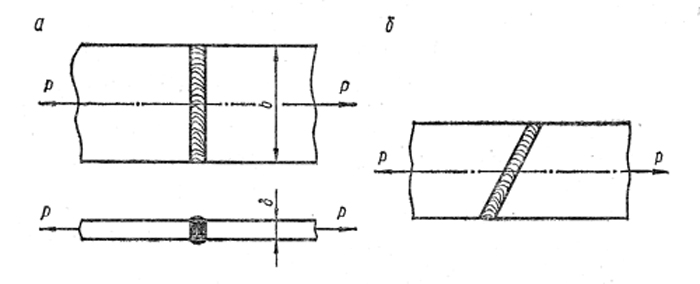
Сварной шов при соединении встык (рис. 1) работает на растяжение и сжатие. Все виды подготовок кромок считаются эквивалентными.

Условие прочности шва (формула 1).

Угловые швы (рис. 2) рассчитываются на срез по сечению, проходящему через биссектрису прямого угла. Расчетная высота шва h = k cos 45° ~ 0,7k.

При несимметричном расположении швов относительно линии действия силы Р (рис. 3) усилия, возникающие в них, определяются из уравнений статики.

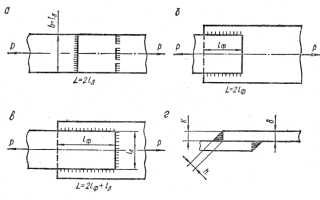
Сварные швы при соединении втавр рассчитываются по-разному в зависимости от типа швов (рис. 4).

Пробочные соединения (рис. 5, а) рассчитываются на срез по формуле.

При соединении деталей точечной сваркой сварной шов работает на срез или на отрыв.

Шов, получаемый роликовой сваркой, рассчитывается на срез.

Расчет прочности швов, нагруженных перпендикулярно стыку свариваемых деталей

Рис. 6. Соединение, нагруженное силой и моментом (стыковые швы)

Расчет прочности стыкового шва, нагруженного силами и моментом (рис. 6), осуществляется по нормальным напряжениям. Влияние поперечной силы, как и при расчете балок на изгиб, не учитывается.

Здесь We = δh²/6 — момент сопротивления сварного шва; Fe = δh — площадь сечения шва.

Рис. 7. Соединение, нагруженное силой и моментом (угловые швы)

При использовании угловых швов (рис. 7) расчет выполняется по условной методике, геометрически суммируя напряжения от изгиба и растяжения с напряжениями, соответствующими поперечной силе.

Величина τQ учитывается только в случаях, когда поперечная сила значительна, а плечо внешнего момента небольшое. В формуле учитываются:

Wc = 2×0,7kh²/6 — момент сопротивления биссекторного сечения швов; Fc = 2×0,7kh — площадь сечения швов.

Расчет прочности швов, нагруженных в плоскости стыка свариваемых деталей

Угловые швы соединения рассчитываются по одной из двух методик: по полярному моменту инерции или по осевому моменту инерции.

В первом случае касательное напряжение определяется по формуле:

[ tau = frac{M cdot r{max}}{I{pc}} ]

где:
— ( M ) — расчетный момент,
— ( r{max} ) — расстояние от центра тяжести шва до наиболее удаленной точки,
— ( I{pc} ) — полярный момент инерции шва, который вычисляется как:

[ I{pc} = I{ус} + I_{zc} ]

где ( I{ус} ) и ( I{zc} ) — осевые моменты инерции шва относительно осей y и z.

Касательное напряжение в любой точке направлено перпендикулярно к радиус-вектору, соединяющему эту точку с центром тяжести периметра шва. Моменты инерции рассчитываются для биссекторного сечения шва.

Во втором способе касательное напряжение определяется по формуле:

[ tau = frac{M cdot y_{max}}{I} ]

где ( y_{max} ) — расстояние от оси элемента до наиболее удаленной точки шва.

Напряжение от растяжения (или сжатия) рассчитывается по формуле:

[ sigma = frac{F_e}{A} ]

где ( F_e = 0,7 kL ) — общая площадь шва.

При учете влияния поперечной силы напряжение вычисляется только для вертикального шва:

[ tau{вс} = frac{F{вс}}{A} ]

где ( F_{вс} = 0,7 kh ).

Суммарные касательные напряжения в опасной точке шва определяются геометрическим сложением.

Расчет швов точечного соединения проводится по одной из двух вышеперечисленных методик. Усилие в наиболее нагруженной точке от внешнего момента суммируется с усилием, равным:

[ P = F ]

Условием прочности служит выражение:

[ sigma leq sigma_{доп} ]

При расчете швов на переменную нагрузку вводится коэффициент ( gamma ) для снижения допускаемого напряжения:

а) для стыковых швов при переменной нагрузке по величине, ( gamma = 1 ); при нагрузке, меняющейся по величине и направлению;

б) для угловых швов при нагрузке, как переменной по величине, так и по величине и направлению.

( P{min} ) и ( P{max} ) — наименьшее и наибольшее по абсолютной величине усилия, которые подставляются в формулы со своими знаками.

Допускаемые напряжения при расчете сварных швов обозначаются как:

[ [sigma]_{р} ] — допускаемое напряжение для основного металла на растяжение.

Расчет угловых сварных швов на прочность, общие положения

Сопротивление металла сдвигу или срезу при действии касательных напряжений значительно меньше, чем сопротивление растяжению, сжатию или изгибу при действии нормальных напряжений. Поэтому расчет угловых сварных швов (на условный срез) сводится к определению касательных напряжений, которые должны быть меньше расчетного сопротивления.

Разрушение углового сварного шва может произойти в двух плоскостях: по металлу шва и по границе сплавления. Поэтому расчет угловых швов выполняется для этих двух сечений.

Рисунок 529.3. Расчетные сечения угловых швов

Теперь рассмотрим возможные напряженные состояния элементов, соединяемых угловыми швами, более подробно.

Расчет угловых сварных швов производится по следующим формулам:

1. Расчет угловых швов при центральном растяжении (рисунок 529.2.д)) или сжатии (действии силы N)

Рисунок 529.2. Основные виды сварных соединений с угловыми швами.

Лобовые и фланговые швы рассчитываются на условный срез.

1.1. по металлу шва (сечение 1 на рисунке 529.3):

twf = N / (βf kf lw) ≤ Rwf γc (531.1)

где N — продольная растягивающая (или сжимающая) сила, приложенная по оси, совпадающей с центром тяжести сечения (без эксцентриситета). Измеряется в кгс, тс, Н, кН;

β_f — безразмерный коэффициент, определяемый по таблице:

Таблица 529.2 (согласно СНиП II-23-81* «Стальные конструкции»)

Примечание: Рекомендую использовать эту таблицу, а не актуализированную редакцию СНиПа, что подробно объясняется в статье о сварных швах.

k_f — катет углового шва. Определяется по конструктивным требованиям или расчету. Измеряется в мм или см.

l_w — суммарная длина угловых швов с учетом непровара в начале и конце. Например, для одного углового шва длиной l расчетная длина составит:

l_w = l — 2t (529.1.1)

где t — толщина наименьшей из свариваемых деталей.

Произведение βf kf l_w — это площадь рассматриваемого сечения.

R_wf — расчетное сопротивление срезу по металлу шва. Определяется по таблице:

Таблица 530.2. Расчетные сопротивления сварных соединений (согласно СП 16.13330.2011 «Стальные конструкции»)

Примечания:

1. Значения коэффициентов надежности по металлу шва γ_wm:

   • γwm = 1,25 — при Rwun ≤ 490 Н/мм² (4900 кг/см²);
   • γwm = 1,35 — при Rwun ≥ 590 Н/мм² (5900 кг/см²).

Значения Rwun и Rf определяются по таблице:

Таблица 531.1 (согласно СП 16.13330.2011 «Стальные конструкции»)

Примечание: В устаревшем СНиП II-23-81* и старых справочниках таблица 530.2 имела следующие примечания:

1. Для угловых швов, выполненных ручной сваркой, значения Rwun равны временным сопротивлениям разрыву металла шва (σв) согласно ГОСТ 9467-75*.

Не буду приводить таблицу из ГОСТа для определения временного сопротивления разрыву шва. Укажу, что в маркировке электродов это значение указано в кгс/мм². Например:

• для электродов Э38 Rwun = σв = 38 кгс/мм² (3800 кгс/см²);
• для электродов Э42А Rwun = σв = 42 кгс/мм² (4200 кгс/см²) и так далее до Э150 (в настоящее время такие марки электродов не рассматриваются).

Это удобно, но сейчас принято выражать значения в единицах системы СИ, что отражено в таблице 531.1.

γ_c — коэффициент условий работы элементов конструкций и соединений, принимаемый по таблице:

Таблица 530.3. Коэффициенты условий работы элементов и соединений стальных конструкций (согласно СП 16.13330.2011 «Стальные конструкции»)

1.2. По металлу границы сплавления (сечение 2 на рисунке 529.3):

twz = N / (βz kflw) ≤ Rwz γ_c (531.2)

где β_z — безразмерный коэффициент, определяемый по таблице 529.2.

Rwz — расчетное сопротивление металла на границе сплавления, определяемое по таблице 530.2. Здесь Run — нормативное сопротивление проката, указанное в следующей таблице:

Таблица 171.8 (согласно ГОСТ 27772-88 для стальных конструкций зданий и сооружений).

Примечание: заменяемые марки стали указаны отдельно.

При центральном растяжении или сжатии элемента из свариваемых деталей во фланговых швах на обеих катетах шва действуют касательные напряжения. В лобовых швах на одном из катетов возникают растягивающие или сжимающие нормальные напряжения, равные касательным напряжениям на втором катете.

Важно отметить, что в справочниках напряжения, определяемые для других видов напряженно-деформированного состояния, иногда обозначаются как нормальные, т.е. литерой «σ». Формально это не является большой ошибкой и делается для различения напряжений, возникающих при действии изгибающего момента и других воздействий. Однако расчет производится именно на условный срез, т.е. на действие касательных напряжений, которые равны нормальным на втором катете. Направления действия касательных напряжений могут различаться, что будет показано далее.

2. Расчет сварных соединений с угловыми швами при действии изгибающего момента М в плоскости, перпендикулярной плоскости расположения швов

В данном случае речь идет о том, что через рассматриваемые швы можно провести плоскость, перпендикулярную плоскости действия момента. Эта формулировка не относится к положению плоскости, в которой может произойти разрушение шва.

Такая ситуация обычно возникает при расчете сварного соединения втавр с двухсторонними швами (рисунок 529.2.г) или односторонними швами (рисунок 529.3). Угловые швы рассчитываются на условный срез.

2.1. по металлу шва (сечение 1 на рисунке 529.3):

2.2. по металлу границы сплавления (сечение 2 на рисунке 529.3):

М/Wz ≤ Rwzγc (531.4)

где М — изгибающий момент, определяемый по эпюре «М».

Wf и Wz — моменты сопротивления расчетных сечений сварного соединения по металлу шва и по границе сплавления с металлом соответственно.

При соединении втавр двухсторонними швами моменты сопротивления составляют:

Wf = 2(βfkflw²/6) = βfkflw²/3 (531.3.1)

Wz = 2(βzkflw²/6) = βzkflw²/3 (531.4.1)

Разделив момент М на момент сопротивления W, мы можем определить нормальные напряжения. В некоторых старых учебниках и справочниках (например, А.П. Мандриков, «Примеры расчета металлических конструкций», М.-1991) формулы (531.3) и (531.4) записаны в другой форме:

σwf = М/Wf ≤ Rwfγc (531.3.2)

σwz = М/Wz ≤ Rwzγc (531.4.2)

Однако суть остается прежней.

Примечания:

1. В СНиП II-23-81* и старых справочниках значение расчетного сопротивления Rwf и Rwz при всех расчетных случаях дополнительно умножалось на коэффициенты условий работы шва γwf или γwz соответственно. Эти коэффициенты принимались равными 1, кроме конструкций в климатических районах I1 (очень холодный, среднемесячная температура воздуха в январе от -50 до -30), I2 (холодный, температура от -30 до -15), II2 (арктический восточный, температура от -28 до -18) и II3 (арктический западный, температура от -30 до -2). Для них γwf = 0.8 при Rwun = 410 МПа и γwz = 0.85 для всех сталей. Это ограничение вводилось для снижения риска хрупкого разрушения сварного соединения при низких температурах. Хотя сейчас оно не действует, важно о нем знать.

2. Это примечание следовало сделать в первом разделе, но он уже получился перенасыщенным информацией, поэтому оставляю его здесь.

3. Расчет угловых швов при действии изгибающего момента М в плоскости, перпендикулярной плоскости швов и действии продольной силы N

Подобная ситуация часто возникает при расчете опорных площадок, поэтому я выделил ее в отдельный раздел, хотя в СП 16.13330.2011 этот вариант загружения не рассматривается.

При приложении силы с эксцентриситетом к опорной площадке возникает следующая ситуация, которую я проиллюстрировал на рисунке из работы А.П. Мандрикова:

Рисунок 531.1.

В этом случае угловые швы рассчитываются на условный срез.

3.1. по металлу шва:

3.2. по металлу границы сплавления:

(тwz² + σwz²)¹/² ≤ Rwzγc (531.6)

Значение касательных напряжений определяется по формулам (531.1) и (531.2) в зависимости от рассматриваемого сечения, а условно нормальные напряжения — по формулам (531.3.2) и (531.4.2).

Примечание:

Согласно требованиям действующих нормативных документов, правильнее говорить о касательных напряжениях относительно осей x и y. То есть тwf = тy, σwf = тx и так далее. Однако, как уже упоминалось, это не влияет на окончательные результаты расчета, а старый подход выглядит более наглядным.

4. Расчет угловых швов при действии изгибающего момента М в плоскости сварных швов

Подобная ситуация часто возникает при расчете стыковых соединений с накладками, когда одновременно используются лобовые и фланговые швы (см. рисунок 529.2.в), а также при соединении внахлест с лобовыми или фланговыми швами (см. рисунок 529.2.а и б). Это означает, что касательные напряжения действуют как вдоль оси x, так и вдоль оси y. Задача сводится к определению равнодействующей этих двух напряжений. Расчет выполняется по следующим формулам:

4.1. по металлу шва:

tM = M(√(x² + y²)) / (Ifx + Ify) ≤ Rwfγc (531.7)

4.2. по металлу границы сплавления:

tM = M(x² + y²)^(1/2) / (Izx + Izy) ≤ Rwzγc (531.8)

где x и y — координаты точки сварного соединения относительно главных осей x-x и y-y. Обычно эта точка максимально удалена от центра тяжести O расчетного сечения.

Ifx, Ify, Izx, Izy — моменты инерции рассматриваемых сечений швов относительно главных осей.

Поскольку швы находятся в одной плоскости с действующим моментом, для определения моментов инерции необходимо учитывать не только катет, длину шва и соответствующие коэффициенты, но и расстояние между швами. Это не требовалось при анализе швов, расположенных в плоскости, перпендикулярной плоскости действия момента.

В нормативных документах вопрос определения моментов инерции для угловых сварных швов не рассматривается. Однако это сложная тема, и ей следует посвятить отдельную статью. Пока ограничимся следующим примером:

При соединении внахлест только лобовыми швами и расстоянии между центрами тяжести лобовых швов, равном l (центры тяжести и расстояние l на рисунке 529.2.а не показаны), значения моментов инерции для сечения металла шва составят:

Ifx = 2βfkflw³/12 = βfkflw³/6 (531.9)

Ify = 2βfkf³lw/12 + 2(l/2)²βfkflw = βfkf³lw/6 + l²βfkflw/2 (531.10)

5. Расчет угловых швов при действии момента М, продольной N и поперечной V сил в плоскости сварных швов

Это общий случай напряженно-деформированного состояния, проиллюстрированный в СП 16.13330.2011:

Рисунок 531.2. Расчетная схема сварного соединения с угловыми швами при общем виде нагрузки.

Расчет выполняется по следующим формулам:

5.1. по металлу шва:

5.2. по металлу границы сплавления:

тz ≤ Rwzγc (531.12)

где тf и тz — касательные напряжения в точке расчетного сечения сварного соединения по металлу шва и границы сплавления, определяемые по формуле:

т = √((тN + тМх)² + (тV + тМу)²) (531.13)

где тN и тV — касательные напряжения, вычисляемые по формулам (531.1) и (531.2), а тМх и тМу — горизонтальная и вертикальная составляющие касательных напряжений при действии момента, определяемые по формулам:

тМх = Мх/Iy (531.14)

тМу = Му/Iх (531.15)

Кроме того, при проектировании строительных конструкций необходимо учитывать конструктивные требования к сварным соединениям.